The United States of America

Home Page

THE PARALLEL PRODUCTION SYSTEM

BY

FRANK LOPEZ

B.S., Purdue University, 1986

THESIS

Submitted in partial fulfillment of the requirements

for the degree of Master of Science in Computer Science

in the Graduate College of the

University of Illinois at Urbana-Champaign, 1987

Urbana, Illinois

ACKNOWLEDGEMENTS

I would like to thank my advisor, Ralph Johnson,

for his patience, advice and continual support.

Also, I would like to thank America for

giving me this opportunity to follow my dreams.

TABLE OF CONTENTS

Chapter 1. Introduction

1.1 Previous work

Chapter 2. Expert Systems

Chapter 3. Production Systems

3.1 Data Driven

3.2 Goal Directed

3.3 Components of a Production System

3.3.1 Productions

3.3.2 Working Memory

3.3.3 Interpreter

Chapter 4. Current Parallel Architectures

Chapter 5. Match

5.1 Rete Algorithm

5.2 Parallelism in Match Phase

5.3 PPS Matching Strategy

Chapter 6. PPS Model

6.1 Design Summary

6.2 PPS System

6.3 Expert Objects

6.3.1 Abstract SIMD

6.3.2 Expert Object definition

6.4 Execution Cycles

6.5 Conflict Resolution Algorithms

Chapter 7. System Manager

7.1 Compile time

7.1.1 Granularities of Parallelism

7.1.2 Processor Resources

7.2 Run time

Chapter 8. Pattern Matching Algorithm

8.1 OPNET

Chapter 9. Implementation Notes

9.1 Compile time

9.2 Multimax

Chapter 10. PPS Prototype Syntax

10.1 Syntax Review

10.2 Grammar

10.3 Syntax Notes

Chapter 11. REFERENCES

Introduction

The Parallel Production System (PPS) is a domain-independent, data-driven, parallel production system developed at the University of Illinois. This system gives users the capability to create modular expert systems on single or multiprocessor architectures. The modules are defined as communicating knowledge sources called Expert Objects. PPS's power comes from two primary sources. The first source is PPS's ability to hide the actual physical architecture of the computer from the user, for an application written in PPS is automatically adapted to the physical architecture of the computer by the PPS System Manager. PPS has two natural parallelisms built into its semantics: one at the Expert Object level, and the other at the rule set level. The second source of power comes from the simple yet powerful PPS language. PPS semantics gives the user the power to easily create any conceivable type of blackboard structure (graph). A user can draw a graph of how the Expert Objects are to communicate, and then easily specify the structure with PPS.

PPS was specifically designed to handle such problems as circuit synthesis that may require propagating constraints through a complex system of objects. Since an Expert Object in PPS can have one or more rules, it can be as simple as an AND-gate object in a VLSI simulator, or as complex as a microprocessor object that simulates an iAPX286. Some perceived applications for PPS include: circuit simulation, silicon compilers, expert systems, and any application where a set of communicating intelligent objects can be utilized as in the design of filters, switching networks, and systolic arrays. PPS can also be used as an efficient OPS5 type production system by simple using only one Expert Object. A prototype parallel version of PPS is currently running on an Encore Multimax.

Previous work

The author's current work is an extension of his previous research at NASA: "CLIPS: C Language's Integrated Production System." CLIPS was an attempt to create a portable production system that didn't suffer from the draw backs of being written in LISP. CLIPS has a full interface to the C programming language, and also takes care of its own memory management. The language is a readable and usable production system with capabilities approaching those of OPS5.

Some of the ideas used in PPS are extensions of previous research done by Charles Forgy. This includes the Rete algorithm [7] and the parallelism of production systems.[5,6] Other work that is similar to PPS includes YAPS [1], ORBS [4], and (PS)²Mⁿ [18].

Expert Systems

Expert systems are computer programs that draw upon the organized expertise of one or more human experts. Human experts tend to explain how they solve problems using heuristics ("rules of thumb"). Therefore if a computer system could learn when to use these same rules then it would be considered just as much an expert as any of the human experts its knowledge came from. These rules abstractly have the form: "if <something is true> then <perform some action>", and are called productions.

An expert system that is fabricated using a production system codes the heuristics of an expert domain into productions. These rules are applied to the current state of the decision making process. The input to the system consists mostly of data objects that describe changes to the current state of the reasoning process. Once the system knows which rules have their conditions satisfied, it has to decide which of these to apply to the current state to generate the next state in the reasoning process. The actions associated with the selected rule(s) are executed each time a rule is applied.

By coding an expert's knowledge into productions we are able to easily update and modify any rules of the system. Furthermore, if the computer system gives a bad response, or a response that could have been better, it becomes a relatively easy task to locate the set of rules that lead to the incorrect decision. As can be seen by the example PPS production given below, the heuristics the system uses have a declarative and modular representation which lends itself to the normal way humans go about solving problems.

(defrule save_baby_1 (declare (priority 99)

;if

(the baby is crawling across the road)

;and

(a Mack Truck is approaching it)

=> ;then

(assert (get the baby out of danger)))

This production could be a member of a set of productions that all dealt with protecting a baby from potential dangers. By giving each rule a priority the system can determine which rule has the most certainty of giving the correct decision.

A major problem of current expert system technology is dealing with the complexity of large systems of rules that simultaneously interact on the same problem. PPS helps deal with this complexity by adding another level of modularity to the problem solving paradigm. PPS allows levels of abstraction in the construction of an expert system. In PPS an expert system can be composed of many sub-experts that are all experts at sub-problems of the overall problem. Each of these experts can then be subdivided, and with each new subdivision of the complexity the system should become more manageable.

A similar problem was encountered in the early days of computers when all programming was done in assembly language. At that time it was difficult to write even the most basic programs due to the enormous complexity associated with writing them in a flat assembly language format. Higher level languages such as Fortran and Lisp were built to make the programming of large problems easier. They did this by providing mechanisms to partition the problem; PPS does the same for production systems.

Production Systems

An expert system encoded as a production system is usually made up of three parts: a set of productions held in production memory, a set of data objects (assertions) held in working memory (blackboard/data memory/current state/knowledge base), and an interpreter (inference engine). There are two primary types of productions systems: data-driven (forward chaining) and goal-directed (backward chaining). Both types of systems have many variations, including some systems that do both types of inferencing.

Data Driven

A data-driven production system uses the contents of the knowledge base to determine which productions can be executed. Therefore by having the knowledge base describe the current state of some process, the productions can then infer new states from the existing state. In an expert system these states describe the current state of the reasoning process, and the state transitions represent the application of an expert's expertise to the knowledge base. In reality we are taking a given situation and applying the rules we know that pertain to it. Each time we apply a set of rules we come up with a new state. Eventually we either draw some valid conclusions, or we determine that the current state is based on incorrect assumptions and therefore is invalid. The creation of multiple current states allows one to choose the best state at any given instance of time, and thus stop the inferencing on any states that are known to be wrong.

Goal Directed

A goal-directed production system backward-chains the inferencing process. This is done by assuming that a goal is true and then attempting to reverse engineer the application of the heuristics of the expert domain. If all the knowledge exists in the system to support that a given asserted goal is true, then the goal becomes one of the possible solutions of the system. This is a guessing algorithm since we guess what the answer is (goal), and then attempt to prove that it is a valid solution. In reality this is equivalent to saying: "this is what I think happened, now can it be supported?" By backward chaining the new states with known data and rules we are able to rule out states that cannot be supported by the knowledge base.

Components of a Production System

A production system has three main components: productions, working memory, and an interpreter. The descriptions given here are of a data-driven production system, since that is what PPS is.

Productions

The first component of a production system is the set of productions. A production is a condition-action construct. Each production has a name, LHS (left hand side/antecedent/condition) and a RHS (right hand side/consequent/action). The LHS is the logical AND of the conditional elements of the production. There are two types of condition elements usually found in the LHS of a production: tests and patterns. The test condition is usually a test for constraints on the pattern conditions that have been satisfied. A pattern condition is satisfied when it matches a data object found in the working memory. Once each element of a rule's LHS is satisfied, the rule is said to be "ready to fire". Each cycle of the production system's execution may produce one or more rules which are in the "ready to fire" state. This set of satisfied rules is called the conflict set, and the production system's conflict resolution algorithm determines which elements of the conflict set will be fired. When a rule is fired its RHS is executed and it is removed from the conflict set. This entire process is called the recognize-act cycle. The production system first recognizes the rules that are in the conflict set, then uses the conflict resolution algorithm to choose instantiations from the conflict set, and finally executes the RHS's of the productions associated with the selected instantiations.

Working Memory

The Working Memory (WM) is a collection of data objects that represents the current state of the system. A production system's working memory is like a classroom blackboard. Each production watches the blackboard for new information. As new information (data objects) streams onto the board, a production determines all of the possible ways its LHS can be satisfied. For each possible way that the production's LHS can be satisfied, an instantiation of the production is placed into the conflict set. An instantiation is an ordered pair of a production and the working memory elements that satisfied the production's LHS. An instantiation is removed from the conflict set when it is fired, or if any of the working memory elements that created the instance no longer exist. The initial state of the working memory is defined by the user, and is modified using a production's RHS operators. Data objects are asserted into the working memory using an assert operator, and are retracted from the working memory using a retract operator.

Interpreter

The interpreter of a production system cycles through the recognize-act cycle. The interpreter must first match the contents of the working memory to each rule's LHS. The interpreter creates the conflict set by finding all of the productions that have become instantiated from the current working memory. Once all of the matching has been done, and a conflict set created, the interpreter uses the conflict resolution algorithm to determine the set of instantiations that it will fire. Once these instantiations have been fired, the interpreter repeats the cycle. System execution terminates when the conflict set is empty after the match phase. This is true because only the RHS of an instantiated production can modify the working memory.

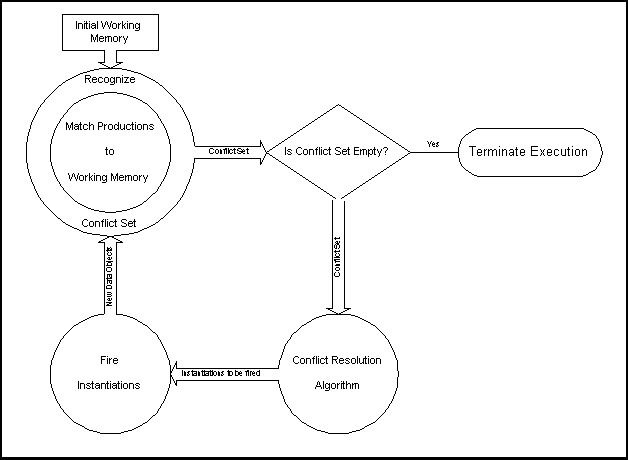
Figure I: A Production System's Recognize-Act Cycle

Current Parallel Architectures

Since the advent of the microprocessor, machine architectures with hundreds and potentially thousands of Processing Elements (PEs) have reached the market. Current researchers seem hard pressed to put all this new processing power to productive use. PPS utilizes multiprocessor architectures to increase the execution speeds of production system applications.

PPS simulates a particular abstract parallel architecture on whatever physical architecture is available. An application written in PPS, for any computer, will work with any other PPS compiler regardless of the underlying computer architecture. This portability is created by having PPS always build an abstract parallel architecture that models the true flow of system execution. One of the System Manager's tasks is to allocate resources for the operation of this abstract parallel architecture.

This design may not fully utilize the physical architecture's potential power, but in this day and age no software is even coming close to fully utilizing the power of every parallel architecture. While some applications can be hand coded to use an architecture, this is expensive and the applications tend to be limited and unportable. PPS tries to naturally maximize the parallelism of an application. The user codes the problem exactly as it is seen, and PPS does its best to utilize all of the inherent parallelism in the user defined system. Consequently, savings in software development costs should be recognized, and at the same time parallelism will be exploited.

Many papers have been written that have shown where potential parallelism exists in production systems, but nobody seems to have written a production system language that takes advantage of these natural parallelisms. PPS was specifically designed to take advantage of the inherent parallelism found in production systems, in addition to any inherent parallelism of the applications written in the language.

Match

The most expensive part of a production system's execution-cycle tends to be the match phase. It is estimated that some production systems spend more than ninety percent of their total run-time in this phase [7]. This problem can easily be recognized since every pattern condition of the LHS of a rule has to be matched to the contents of the working memory. If the working memory has many data objects and the system has many productions, then the amount of time that could foreseeably be spent would be equal to that of matching every pattern condition to every data object on each execution-cycle. However, PPS uses an efficient pattern matching algorithm that trades memory for faster execution speeds.

Rete Algorithm

The PPS pattern matching algorithm was derived from the Rete Algorithm [7]. This efficient pattern matching algorithm will only once match a pattern condition to a data object for the entire life-span of the data object. A data object is compared to every pattern only when it is first placed in the working memory. This is accomplished by saving previous match information in a logical net that represents the LHS of a rule. More about how this works is left for chapter eight.

Parallelism in Match Phase

Pattern matching is only a small piece of the match phase. In addition, interpattern variable bindings have to be unified, and test element conditions have to be checked. All of these things are associated with successful matches, but are not directly associated with the actual pattern matching. In the Rete algorithm these steps can take up a large percentage of the match time, and worst, the time cannot be predicted since the number of new data objects that will match a particular pattern cannot be predicted by the system. Fortunately the Rete algorithm is setup so that this nonpattern-matching work can be partitioned with the patterns, and therefore the entire matching phase can be done in parallel. The list of patterns with the information to perform the nonpattern-matching work is called the pattern-list. Each production has its own pattern-list. Furthermore, pattern-lists are closed under concatenation. Initially all of the Expert Object's rules have their pattern-lists concatenated into a single pattern-list.

The matching process contains three ingredients: new data objects, processors, and the patterns to be matched. There are two primary ways of using parallelism for match algorithms.

The first parallel match algorithm assigns a single processor to match each new data object against the entire pattern-list. This algorithm would appear to be efficient if the average number of new data objects, on each recognize-act cycle, is equal to that of the number of processors available for matching. A disadvantage is that there may be a large percentage of idle processors if the average number of new data objects is much less than the number of available processors.

The second parallel match algorithm assumes that the pattern-list is partitioned according to each processor's capability. Since each of these partitions are in fact system defined rule sets, they cannot be created within the pattern-list of a rule's LHS. This algorithm sends new data objects in parallel to each partition's input buffer, and then each processor matches each data object to its pattern-list partition. If this partitioning is done judiciously then a high degree of parallelism can be utilized in each Expert Object, for each of an Expert Object's rules can be run on its own processor. A disadvantage is that it is difficult to create proportionately equal pattern-list partitions.

PPS Matching Strategy

PPS uses both types of algorithms. The patterns are partitioned into approximately equal sets. Each processor is assigned a pattern-list partition and a data-object input buffer. Each time a new data object arrives it is sent in parallel to each partition's input buffer for matching. Once a processor matches all of the data objects in the partition's input buffer, it then checks to see if any other processors still have data objects to be matched. If one is found then the processor grabs a data object from that processor's input buffer and starts matching in parallel with any other processors that are currently working on the partition. We can have the best of both algorithms by making sure that this teaming of processors on a partition is done judiciously.

This can be accomplished by having a floating pool of the processors that have finished processing their partitions. Each processor in this pool is then assigned a data object from a currently running processor's input buffer. A proper assignment should consider any performance improvements that would be derived from the assignment. For instance if too many processors are working on a partition then they may spend most of their time waiting for each other in the partition's critical sections. Also the partition with the most data objects in its input buffer should be assigned processors before any partition with a lesser amount of data objects in its input buffer.

Each pattern-list partition represents a system defined rule set called a partition set. The current pattern-list partitioning algorithm partitions using only rule units. A rule unit is defined as the set of patterns that appear within any rule's LHS. This means that the patterns in a rule's LHS must all appear in the same partition. However, if the partitions are being stored in shared memory then the partition sets will have a pattern unit instead of a rule unit.

A pattern unit means that multiple processors can have exclusive disjoint sets of patterns from a rule's LHS. If shared memory is used then the rule would appear in each of its pattern's partition sets. However, a particular instantiation of the rule would only appear in the conflict set of the partition set that first recognized it. Therefore at any given instance of time a rule can have instantiations appearing in many different conflict sets. Thus the conflict sets of the partition sets are disjoint.

PPS Model

Design Summary

PPS is a parallel production system that was designed to take advantage of any parallelism in production systems and their applications. There are four main aspects to the PPS model:

1. A PPS System is a collection of communicating Expert Objects. The system executes using a synchronous communication protocol.

2. An Expert Object is a standard data-driven production system with the added capability of being able to communicate with other Expert Objects in the PPS system.

3. An Expert Object is implemented as an "abstract SIMD" machine.

4. The System Manager is responsible for the allocation and maintenance of resources for the PPS system. It takes care of any machine dependent features of the PPS model.

PPS System

An expert system written in PPS is a set of communicating Expert Objects. Each expert object has its own working memory and rule set(s). An Expert Object cannot be directly modified by another Expert Object. Any communication between expert objects must be done through communication channels created by the system. At compile-time a unidirectional virtual connection is created between two Expert Objects if the System Manager determines that one Expert Object needs to send messages to the other Expert Object. This need is determined by a compile-time analysis of the right hand sides of all of the rules for each Expert Object.

All of the Expert Objects synchronously send and receive messages. An Expert Object cannot execute until it has received some type of message from each of its input ports. Consequently each Expert Object will always send some type of a message to all of its output ports for each recognize-act cycle. A nonempty message is always the direct result of the execution of the RHS of a rule. A message does not affect the behavior of an Expert Object until the Expert Object retrieves the message from its input port. The messages that can be sent between Expert Objects are:

1. assert - assert a data object into the working memory of an Expert Object.

2. retract - retract a data object from the working memory of an Expert Object.

3. stop - stop the execution of the Expert Object.

Expert Objects

Abstractly each Expert Object (EO) is a knowledge source in the expert system. The EOs communicate through communication channels established by the system. An EO is composed of one or more user defined rule sets.

Rule sets help deal with the complexity of building expert systems. Partitioning rules into rule sets should make the expert system easier to maintain and read. A rule set prevents name conflicts with rules that appear within different rule sets in the same EO. Thus the same rule name can be used multiple times within an EO.

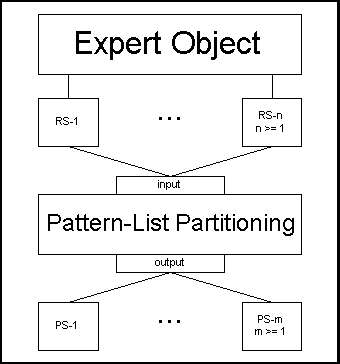
Figure II: Creation of an Expert Object's partition sets

Each Expert Object has its own set of partition sets that are derived at compile-time from its user defined rule sets. This partitioning is done by the pattern-list partitioning algorithm. The union of an Expert Object's user defined rule sets is fed as input to the pattern-list partitioning algorithm. The output from this algorithm is the Expert Object's partition sets (PS) used by the System Manager to transform the Expert Object into an "abstract SIMD" machine.

Abstract SIMD

Single instruction stream-multiple data stream (SIMD) architectures correspond to the array processor class in which there are multiple processing elements that are supervised by the same control unit. "All PEs receive the same instruction broadcast from the control unit but operate on different data sets from distinct data streams."[13]

The term "abstract SIMD" means that the single instructions are not hardware instructions, but rather instructions from the EO's inference engine to its partition sets during the recognize-act cycle. The multiple data streams are created by giving each partition set a unique input data buffer (input data set) that is connected to the control processor via a unique communication channel (data stream). The "abstract SIMD" machine is created and defined by the System Manager at compile-time.

The "abstract SIMD" machine has a control unit (processor) and a set of array processors. The machine's array processors correspond to the Expert Object's partition sets, and the control processor handles the Expert Object's control related features. There are two primary purposes for having a control processor for the partition sets. The first purpose is to interface the partition sets to the PPS system, and the second purpose is to serve as the control inference mechanism for the Expert Object. This strategy was used because it increases the parallelism and modularity of the system, but reduces the system's communication needs.

The primary goal for using an "abstract SIMD" architecture was to make the partition sets independent of one another, yet working as a team on the same problem with the control processor as the team's manager. This was accomplished by giving each partition set a copy of the working memory, a local agenda, and a conflict resolution algorithm. The control processor keeps all of the partition sets working in synchronization, and is solely responsible for all communication to and from a partition set.

Expert Object definition

Each EO is composed of five parts:

1. communication channels - These include connections between the communicating EOs, in addition to the connections created for the Expert Object's "abstract SIMD" machine.

2. distributed agenda - The agenda is the order in which the current conflict set is to be executed. The Expert Object's agenda is distributed throughout its partition sets and is obtained, when needed, by polling the partition sets.

3. working memory - The working memory contains the current data objects of the EO's knowledge base.

4. pattern-list partitions - These partitions are created by the pattern-list partitioning algorithm for the array processors of the "abstract SIMD" machine.

5. inference engine - The control mechanism for the recognize-act cycle.

Each partition set is composed four parts:

1. A local copy of its Expert Object's working memory.

2. A local pattern-list that is the concatenation of each pattern-list of each of the partition set's rules.

3. A local agenda that contains the results of applying the partition set's conflict resolution algorithm on the partition's conflict set.

4. Two communication ports (in, out) for communication with the Expert Object's control processor.

An EO and its partition sets all have their own message processing centers. These centers control all of the input and output from the respective type of object. The processing of messages is one of the main functions of the EO control processor, since messages are used to keep the PPS system synchronized. The partition set's message processing center is used to control the flow of data to and from the PPS pattern matching algorithm that processes the local pattern-list partition.

An EO's control processor has no state information. All of the state information, including the EO's agenda, is stored in its partition sets. Any message sent to a control processor is forwarded to its partition sets. The only type of message that the control processor actually processes is the stop message.

At any time an Expert Object can stop its own processing by sending itself a stop message. A stop message will properly close all of the communication channels that are connected to the Expert Object. However, an EO can only stop itself after it has stopped all of its partition sets.

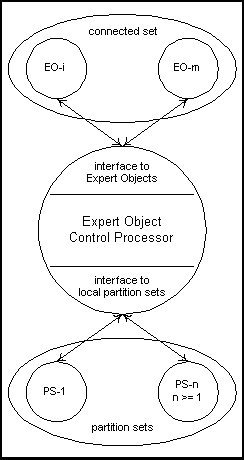
Figure III: A PPS Expert Object

Figure III is an example of an Expert Object. In this example, the System Manager has determined that EO-i and EO-m both have the capability to send messages to the Expert Object, and that the Expert Object has the capability to send messages to EO-i. The Expert Object has communication channels to and from each of its partition sets.

Execution Cycles

When execution begins, the Expert Object initializes its working memory with the user defined data objects. An Expert Object has six steps to its execution cycle:

1. Poll each of the partition sets for conflict resolution information (instantiations).

2. Perform the EO's conflict resolution algorithm on the conflict set sent by the partition sets.

3. Based on the output of the conflict resolution algorithm, instruct the appropriate partition set(s) to fire the rule at the front of their agenda(s).

4. Accept any messages from the partition set(s) whose instantiations were executed in step three. These messages will be processed and forwarded to the addressed EOs. If an EO receives a message from its partition sets that is addressed to itself, then the EO sends the message in parallel to all of its partition sets. If the EO receives a stop message from one of its partition sets then it will send the message to all of its partition sets and then stop itself.

5. Send a message to all its output ports that indicates that the Expert Object has finished its execution cycle. This final message makes sure that every EO that is connected to it via an output port will receive a (possibly empty) message from the EO. This will ensure that each EO knows when to stop waiting and thus prevent deadlock.

6. Accept the messages from all of the EOs that have output ports connected to it. Send any nonempty messages to the partition sets.

The partition set's execution cycle has five steps:

1. Read input messages from the EO.

2. Perform the action specified by the message type (assert/retract/stop). A stop message terminates execution of the partition set.

3. If the EO control processor requests the instantiation at the front of the agenda and the agenda is empty, then send a no_agenda message. If the agenda is not empty then send a message that contains the appropriate information.

4. Wait for the Expert Objects to decide which, if any, local instantiations should be fired.

5. If instructed to fire then execute the rule's RHS and send any messages produced by its execution to the EO control processor.

Conflict Resolution Algorithms

The PPS interpreter generates a conflict set in the recognize phase of the recognize-act cycle. The PPS conflict resolution algorithm determines which elements of the conflict set, if any, are to be executed. This is a distributed conflict resolution algorithm since each partition set performs a conflict resolution algorithm on its own conflict set. Another conflict resolution algorithm is performed by the Expert Object on the information it receives from its partition sets.

A partition set's conflict resolution algorithm orders instantiations by sorting them based on their time stamp, their rule set's priority number, and their production's priority number. The conflict set is sorted first by the priority of the rule's rule-set, and then by the rule's priority, and lastly using the instantiation's time stamp.

In the current PPS system the Expert Object's conflict resolution algorithm is identical to the partition set algorithm. The Expert Object polls each partition set for the portions of its distributed agenda that it needs to determine which rules are to be fired. In future versions of PPS the Expert Object's conflict resolution algorithm may differ from that of the partition sets.

System Manager

The System Manager is all of the PPS software that is machine dependent. PPS can be ported to a new machine (that has a C compiler) by rewriting the System Manager. Regardless of the type of architecture PPS is ported to, the System Manager should always be transparent to the user's application. Consequently, applications do not have to be modified when they are ported from one machine to the next. There are two phases to the System manager: compile-time and run-time.

Compile time

At compile-time the System Manager determines the appropriate degree of parallelism to use. This decision is directly related to the resources available to it, for the "abstract SIMD" machines are created so that they utilize all of the available processors.

The System Manager distributes its processors in three steps.

1. Determine the total number of processors available.

2. If the total number of processors is greater than or equal to the number of Expert Objects then allocate one processor to each Expert Object. Otherwise evenly distribute the Expert Objects to the processors. A processor assigned several EOs will time-share between them.

3. Allocate any remaining processors to the Expert Objects using the pattern-list partitioning algorithm.

Granularities of Parallelism

There are three granularities of parallelism that PPS can exploit: large, medium, and small. The granularities are applied from largest to smallest.

The largest granularity is the use of multiple Expert Objects. Here each Expert Object can be assigned its own processor.

Medium sized granularity involves the automatic partitioning of the user defined rule sets into proportionately equal partition sets. This involves the creation of an "abstract SIMD" machine for each Expert Object. The smallest medium granularity is when each partition set has only one rule unit.

Small granularity is when there are multiple processors assigned to each partition set. Here the processors work in parallel on the same partition. This involves the creation of a processor pool for any idle processors.

Processor Resources

The following variables are used in further definitions.

Let N be the total number of rules in the system.

Let M be the total number of Expert Objects in the system.

Let P be the total number of processors available to PPS.

Let T by the total number of patterns in the system.

The maximum number of processors that the combined large and medium granularity can use is equal to N + M. This figure is derived by creating an SIMD machine for each Expert Object that has one control processor, and one processor for each rule of the Expert Object. The minimum number of processors that can be used is one. Furthermore, when P < M + N a concurrent programming scheme inspired by ORBS (Oregon's Rule Based System)[4] will automatically be used.

If P > M + N then the smallest granularity of parallelism can be exploited. This involves using multiple PEs for the Rete algorithm used for matching the working memory to each partition's pattern-list.

At least T + M processors can be utilized if all three granularities of parallelism are used. Furthermore, if an algorithm could be derived that would allow multiple processors to work together on matching a single data object to a single pattern then the maximum number of processors used would be much greater.

Run time

The run-time implementation depends upon support available from the operating system. If the operating system has the basic features that PPS needs, then the run-time implementation will be very simple. If the operating system is very primitive or doesn't exist, then the System Manager will look more like an operating system. The current run-time tasks are: establish and maintain communication channels in the system, and provide any capabilities that the abstract parallel architecture needs to execute synchronously. Future tasks may include processor fault tolerance, the dynamic creation of Expert Objects, and the ability for the system to fine tune its execution at run-time.

Pattern Matching Algorithm

The PPS pattern matching algorithm was derived from the Rete algorithm. The PPS compiler compiles each production's LHS into a dataflow structure which in PPS is called the OPNET (OPerator NETwork). The OPNET is the internal representation of a production's pattern-list. One OPNET is created for each partition set.

The OPNET is created by linking all of a production's patterns together into a binary tree network. The leaves of the binary tree network are the compiled patterns. A pattern will appear only once in a given OPNET. The internal nodes of the tree network are two-input AND nodes that represent the merge of a pattern with all of the patterns that appeared before it in the LHS of a production. Since one pattern can be included in several productions, a leaf can have several parents. An OPNET has one root node for each of its productions. A root node is called a terminator node.

At run-time a token is created each time a pattern is successfully matched to a data object. Two types of information may be found in this token: variable bindings, and the names of all of the data objects that matched the patterns that the token represents. This token is fed into the OPNET, and will flow as long as it can be merged (unified interpattern bindings) with a token from the opposite input. If a token flows into the terminator node it means that the production whose name is associated with the terminator node is ready to fire. When this occurs an instantiation pair (production, token) is added to the conflict set.

OPNET

Below we give an example of a partition set with two productions. The OPNET that represents their left hand sides is given in figure IV.

In this text the token format is <data object's WM id (,variable binding name = value)*>, and the WM format is <data object's WM id > <data object>.

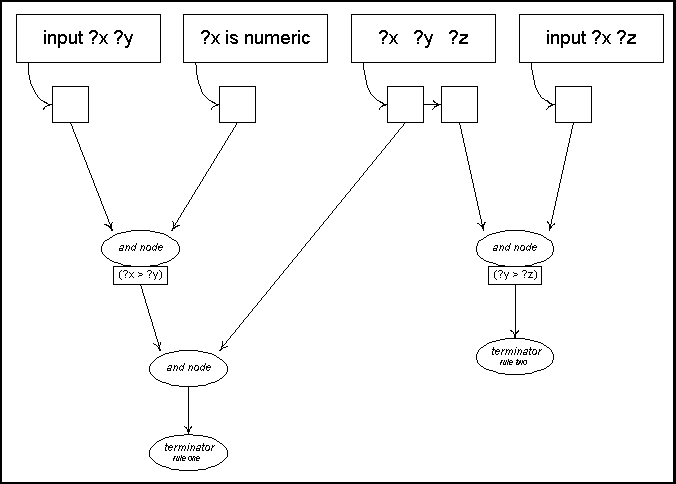
Figure IV: Initial OPNET for rule-one and rule-two

In figure V the working memory in table I has been matched to the OPNET in figure IV. In this example the working memory has six data objects. Each of these data objects is pattern matched to each pattern in the OPNET. A token is created each time a data object successfully matches a pattern. A token remains in an AND node's input buffer until one of the data objects that created it is removed from the working memory by the retract operator.

The matches given in table I represent all of the possible matches of the given WM to the given set of patterns. The token that was produced by the match is indicated in parenthesis after the respective match. A list of all of the tokens produced directly from the matching phase is given in table II. However, more tokens are created when some of the existing tokens are successfully merged at the OPNET's AND nodes. This AND node merging is called interpattern unification. The results of the interpattern unification are given in figure VI and are summarized in table III.

Whenever a new token is created, it flows to the parent AND node. The AND node attempts to merge the new token with each existing token from the opposite side of the node. Every token that is successfully created from this merging process is sent to the next parent node in the OPNET. When a terminator node receives a token, the token and the terminator's production object will together be placed into the conflict set. Above we see that T9 was created from T3 and T5, T11 was created from T9 and T7, and T10 was created from T2 and T7. It is easily seen that no other tokens are produced by the AND nodes.

Instantiations of "rule one" and of "rule two" were created when T11 and T10 flowed into their terminator nodes. If the WM only contained the given six data objects, then these two productions would be the conflict set. The conflict resolution algorithm decides which members of this conflict set are to be fired. The conflict set is checked again only after all of the selected instantiations have been executed. Only new additions or deletions to the WM have to be propagated through the system since all of the old state information is stored at each of the AND nodes.

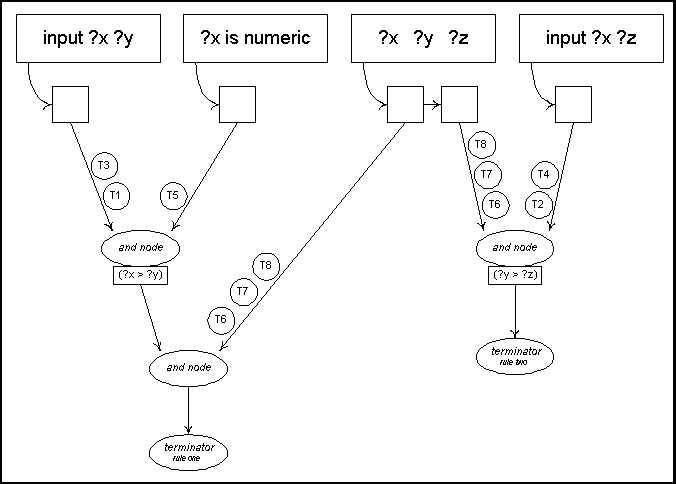
Figure V: Result of matching the WM to the OPNET's patterns

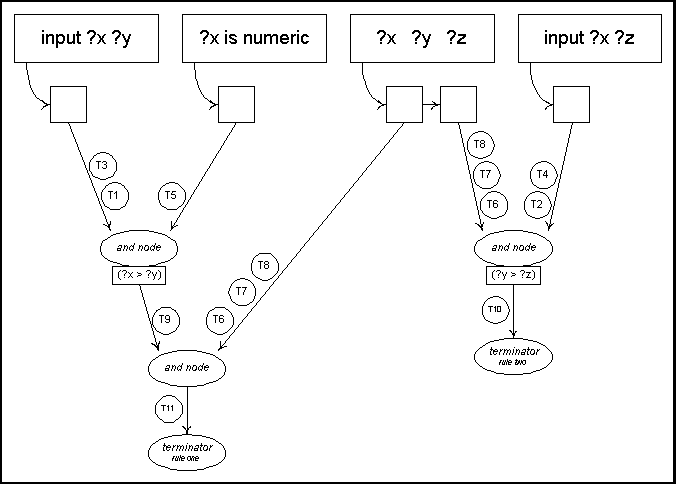
Figure VI: Result of interpattern unification

Implementation Notes

Compile time

At compile-time a number of things are done to set up the system. These are:

1. Analyze the Expert Objects to determine for each Expert Object:

1. The set of Expert Objects that it can receive messages from. In the current implementation a system mailbox is created for each member of this set. The addresses of these mailboxes are mapped to their potential senders so that each sender is given a unique address to send to.

2. The set of Expert Objects that it can send messages to. Each member of this set is assigned a mailbox address after all of the objects in the system have been created.

2. Partition the pattern-list and determine the extent to which each of the three granularities of parallelism can be used. Proceed from largest to smallest and always first try to maximize the larger granularity before using a smaller granularity.

Each data object is issued a unique identification number. Each Expert Object assigns consecutive integers to the data objects that it creates. The concatenation of this number and the Expert Object's identification number is the data object's unique system wide identification number.

Multimax

The first PPS prototype was built on an Encore Multimax. Its main purpose is to show that the PPS design is correct, which it has successfully accomplished.

The Multimax environment allows one to define how many processors are needed (processes; task_init), and then provides mechanisms to start tasks on the processors (tasks, task_start). All tasks share the same address space.

PPS currently starts one process for each Expert Object and partition set. A PPS system processor is then created by running a system defined task with each of the processes. There are two types of tasks that are started: expert objects and partition sets. Each type is started with a structure that specifies its local memory and I/O ports. These structures are created by the System Manager from the parser's output. A barrier is used to start up the whole system in synchronization.

Execution begins when the barrier is released (tasks start execution), and ends only after each task in the system has stopped itself. An Expert Object that has stopped execution cannot be restarted. In addition the prototype will not allow any new Expert Objects to be added to the system after the barrier is released.

The scanner tends to be the most reused piece of code in the system. It is used both at compile-time and during execution. Messages in the system are currently sent using character strings. Any data objects sent to a mailbox must be reparsed by the receiver into a data object format. This requires a scanner with two modes, fetching characters from an input file, and fetching characters from an input string. Regardless of the mode, the behavior of the scanner is identical. An end-of-file token is returned for end-of-string and end-of-file. Inside the scanner the only difference is that the character-fetch function gets the next character from the input string unless there is a currently opened file.

The Multimax PPS system uses a single address space. Some local optimizations that take advantage of this addressing include: string comparisons are done by comparing addresses (use of a hash table), and mailboxes are addressed by their structure's memory address.

A disadvantage of the single address space is that static and global variables have to be properly accessed by any tasks that are running in parallel. In some cases this required the use of critical sections, and in the other cases the variables were packaged into structures that were passed to the functions that used them. For example the scanner is passed a structure that contains a place for the new token and the current input processing state. This was done because the scanner is used in such tasks as message processing and the creation of new data objects; all of which can occur in parallel.

PPS Prototype Syntax

Syntax Review

The current PPS syntax has four main constructs:

1. defeo - The definition of an Expert Object.

2. deffacts - The initial definition of an Expert Object's working memory.

3. defrs - The definition of a rule set.

4. defrule - The definition of a rule (production).

The deffacts and defrs constructs are nested within the defeo constructs, and the defrule construct is nested within the defrs construct. The defeo construct cannot be nested within any type of construct.

Grammar

A Left-Recursive Context-Free Grammar for PPS is:

<pps system> ::= <defeo_lst>

<defeo_lst> ::= <defeo_lst> <defeo> | <defeo>

<defeo> ::= (defeo <name> <eo_stmt>)

<eo_stmt> ::= <eo_stmt> <eo_opt> | <eo_opt>

<eo_opt> ::= <defrs> | <deffacts>

<defrs> ::= (defrs <name> (declare (priority <integer>)) <defrule_lst>) |

(defrs <name> <defrule_lst>)

<defrule_lst> ::= <defrule_lst> <defrule> | <defrule>

<defrule> ::= (defrule <word> (declare (priority <integer>))

<condition_lst> <then> <action_lst>) |

(defrule <word> <condition_lst> <then> <action_lst>)

<condition_lst> ::= <condition_lst> <condition element> |

<condition element>

<condition element> ::= <pattern condition element> |

<test condition element>

<pattern condition element> ::= (<clause>) |

<variable> <binder> (<clause>)

<test condition element> ::= Î

<action_lst> ::= <action_lst> <action> | <action>

<action> ::= <assert> | <retract> | <printout> | <stop>

<retract> ::= (retract (<variable_lst>)) |

(retract (<variable_lst>) <sender> <receivers>)

<assert> ::= (assert (<clause>)) |

(assert (<clause>) <sender> <receivers>)

<printout> ::= (printout (<clause>))

<stop> ::= (stop)

<receivers> ::= <receivers> , <word> | <word>

<deffacts> ::= (deffacts <name> <fact_lst>)

<fact_lst> ::= <fact_lst> <fact> | <fact>

<fact> ::= (<literal_lst>)

<clause> ::= <clause> <element> | <element>

<element> ::= <variable> | <literal>

<variable_lst> ::= <variable_lst> <variable> | <variable>

<variable> ::= ?<word>

<literal_lst> ::= <literal_lst> <literal>

<literal> ::= <word> | <float>

<float> ::= <integer> | <integer>. | <integer>.<integer> |

.<integer> | <integer>.<integer><exp>

<exp> ::= e <integer> | E <integer>

<integer> ::= <integer header> <digit_lst> | <digit>

<integer header> ::= 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9

<digit_lst> ::= <digit_lst> <digit> | <digit>

<digit> ::= 0 | <integer header>

<word> ::= <word header> <string> | <word header>

<word header> ::= [a-z] | [A-Z]

<string> ::= <string><char> | <char>

<char> ::= <word header> | "_" | "-" | [0-9]

<then> ::= "=>"

<binder> ::= "<-"

<sender> ::= "->"

Syntax Notes

The "declare" clause is used to specify an attribute of a construct. It is currently only being used to declare the priority of the rules and of the rule sets.

The constants <integer> and <float> are identical to their counterparts in C. If you ever have problems with these constants then it might help to determine your C compiler's definition of these constants since they are identical to PPS's interpretation.

The <receivers> field in <assert> and <retract> is used to specify what Expert Objects in the system you want these messages sent to.

Comments may be used by specifying a ";" anywhere in the body of the code. Anything that appears between the ";" and the end of the line will be ignored.

REFERENCES

1. Allen, E., "YAPS: A Production Rule System Meets Objects", Proc. of AAAI, August, 1983.

2. Clinger, W.D., "Foundations of Actor Semantics", Ph.D Dissertation, MIT, 1981.

3. de Kleer, J., and Sussman, G.J., "Propagation of Constraints Applied to Circuit Synthesis", MIT AI Lab Memo 485, September, 1978.

4. Fickas, S., "Design Issues in a Rule-Based System", ACM SIGPLAN Notices, 20, 1985.

5. Forgy, Charles, L., "A Production System Monitor for Parallel Computers", CMU SDL-395, April, 1977.

6. Forgy, Charles, L., "On the Efficient Implementation of Production Systems", CMU SDL-425, 1979.

7. Forgy, Charles, L., "Rete: A Fast Algorithm for the Many Pattern/Many Object Pattern Match Problem", Artificial Intelligence, 19, 1982.

8. Forgy, Charles, L., McDermott, J., "OPS, A Domain-Independent Production System Language", Proc. of the 6th IJCAI, August, 1979.

9. Georgeff, M.P., "A Framework for Control in Production Systems", Proc. of the 6th IJCAI, August, 1979.

10. Gu, J., and Smith K.F., "KD2: An Intelligent Circuit Module Generator", IEEE-DA, 1986.

11. Hewitt, C., Baker, H., "Actors and Continuous Functionals", MIT AI Lab Memo 436A, July, 1977.

12. Hewitt, C., Lieberman, H., "Design Issues in Parallel Architectures for Artificial Intelligence", MIT AI Lab Memo 750, November, 1983.

13. Hwang, K., Briggs, F.A., Computer Architecture and Parallel Processing, McGraw-Hill Book Company, 1984.

14. Lenat, D.B., McDermott, J., "Less than General Production System Architectures", Proc. of the 5th IJCAI, August, 1977.

15. McDermott, J., Forgy, C., "Production System Conflict Resolution Strategies", CMU SDL-392, December, 1976.

16. Mizoguchi, R., Kakusho, O., "Hierarchical Production System", Proc. of the 6th IJCAI, August, 1979.

17. Siegel, H.J., Schwederski, T., Davis, N.J., Kuehn, J.T. "PASM: A Reconfigurable Parallel System for Image Processing", Proceedings of the Workshop on Algorithm-guided Parallel Architectures for Automatic Target Recognition, July, 1984.

18. Uhr, L.M., "Parallel-Serial Production Systems", Proc. of the 6th IJCAI, August, 1979.

19. Waterman, D.A., "Adaptive Production Systems", CMU Working Paper 285, December, 1974.